内角 の 求め 方 320996-内角の求め方
1
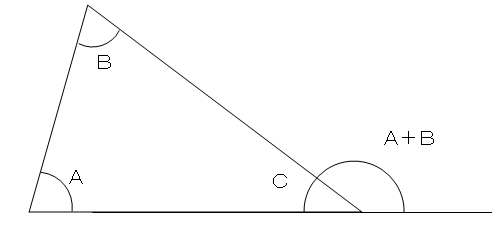
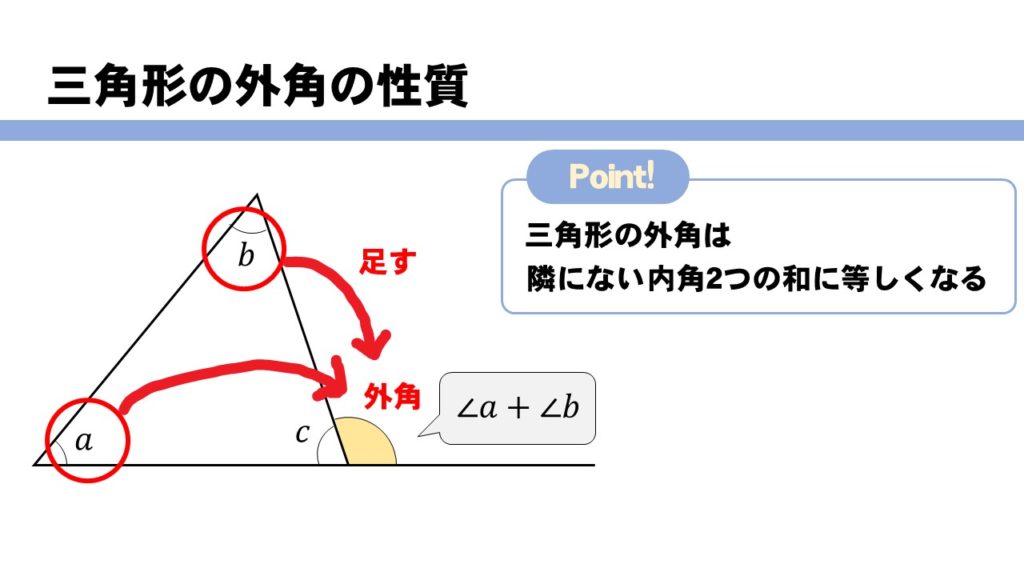
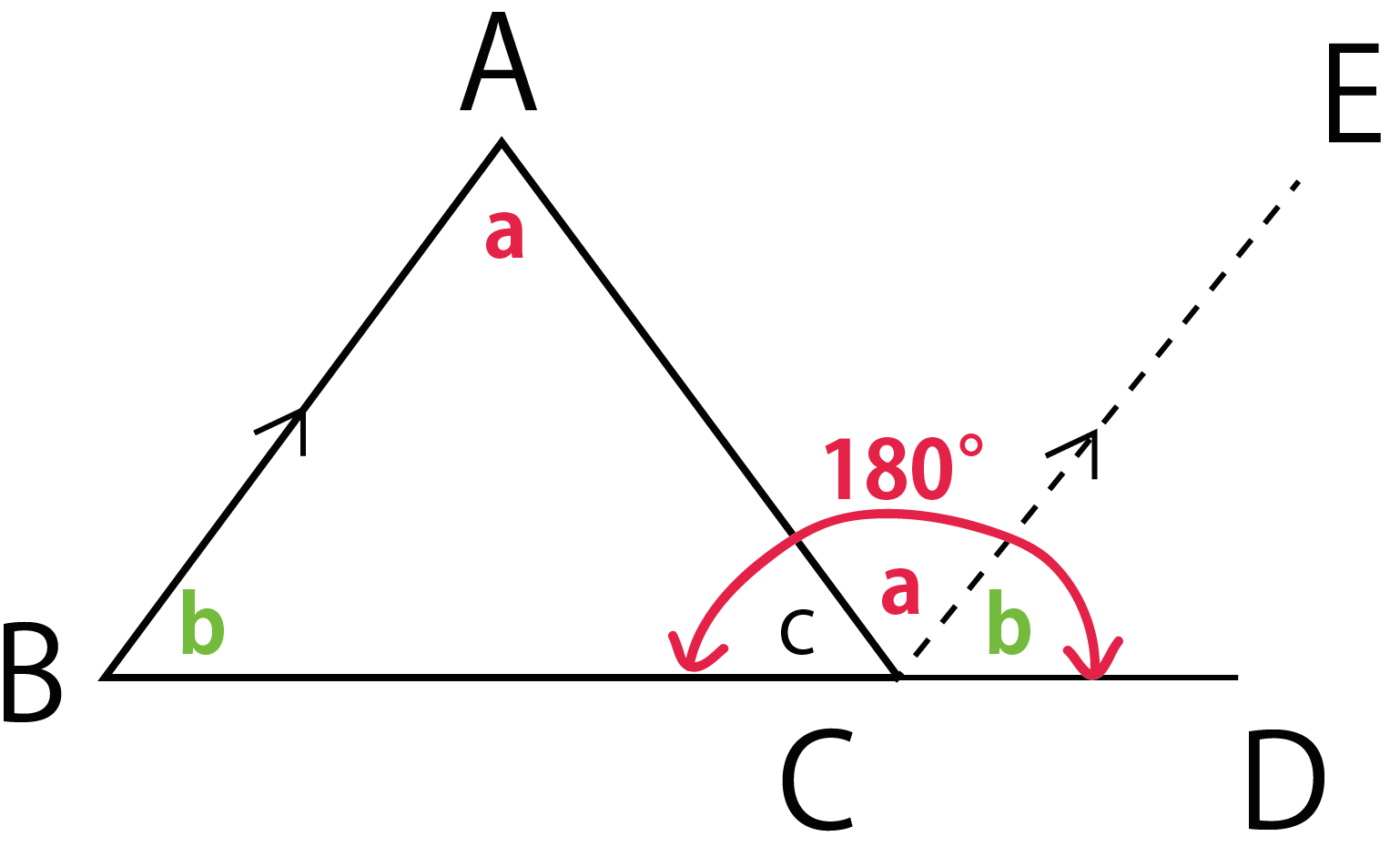
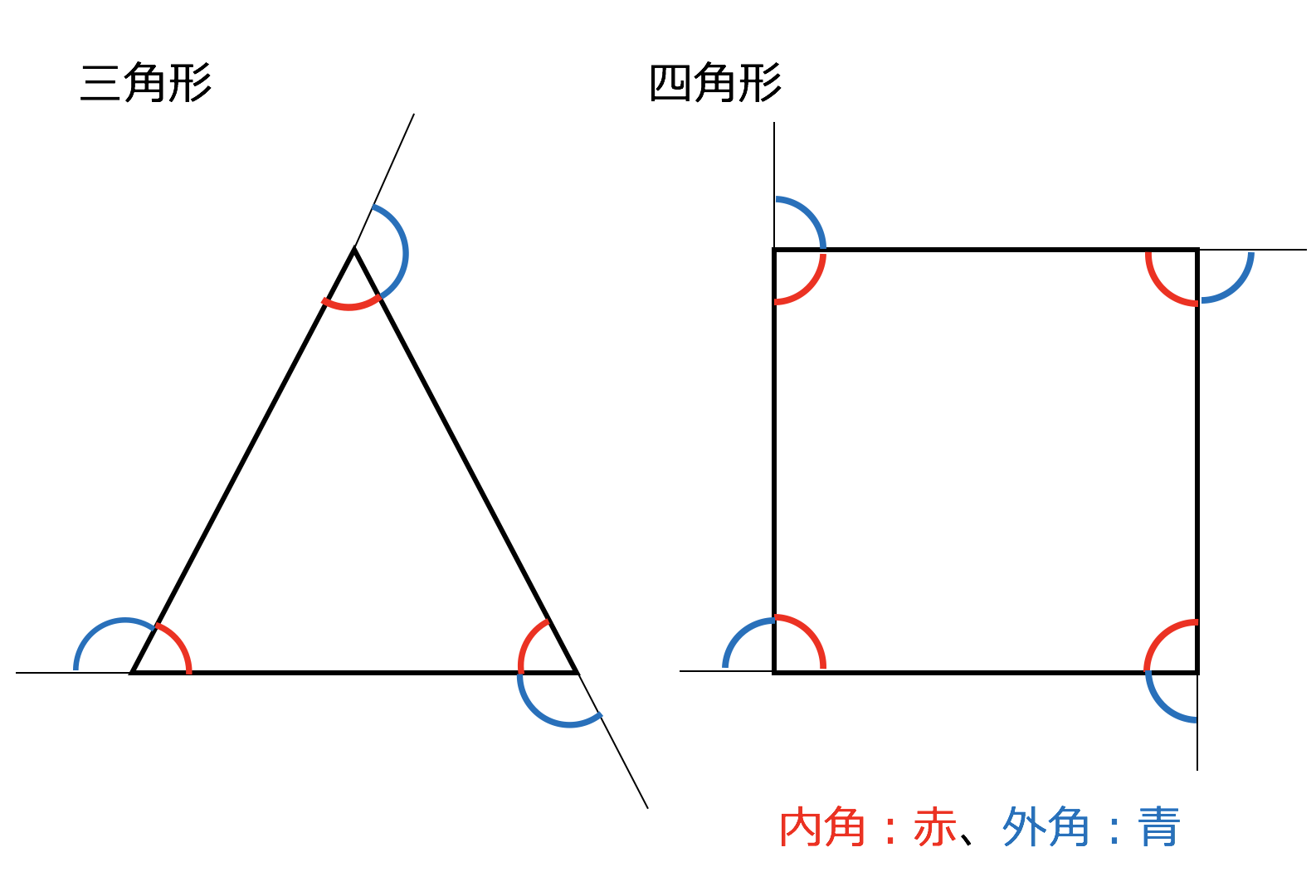
さて、具体的に角Aの余弦、つまり\(\cos A\)を求めてみます。 公式の使い方ですが、実は頭の中では次のように考えて使います。 求めたい角度の対辺はどれか？ 求めたい角度を挟んでいる辺はどれか？ もし、求めたい角がAであるのなら、 対辺はa、三角形の外角の求め方 ① 外角 = 離れた2つの内角の和 ex) c の外角＝ab ② 外角 = 一直線 （ いっちょくせん ） 180° その内角( ←当然) ex) c の外角＝180°c (当然と言えば当然ですね。 三角形の 内角の和 は180°、 一直線 も180°、180°つながりですね！)
内角の求め方
内角の求め方- 下の図で色を塗った部分の多角形（七角形）の外角の和は360°になるので、 の和が360°、また の和も360°となります。 問題の印をつけた部分の和は三角形7つ分の内角の和－ ( の和＋ の和) となり、180°×7－360°×2＝ 540° となります。 内側に三角形タイプ 角の和 内側に三角形ができているタイプでは、 補助線 をひき、リボンの定理を使います。 例題4 下の図のように、図形に 外角の求め方② 外角の大きさ＝ ★ を使ってみよう。 ∠外角＝40°75°＝115° ・・・（答え） ほら同じになるでしょ？！ だから 三角形の1つの外角は、その隣にない2つの内角の和と等しい 外角は対頂角になっている
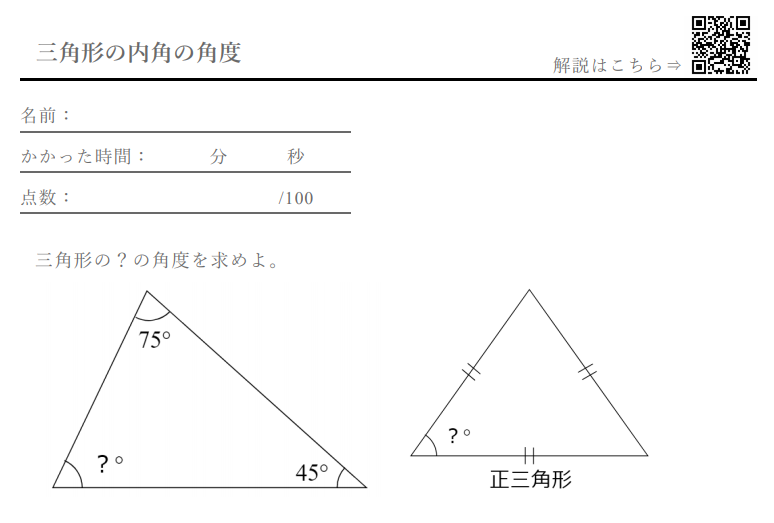
三角形 の内角の角度 計算ドリル 問題集 数学fun
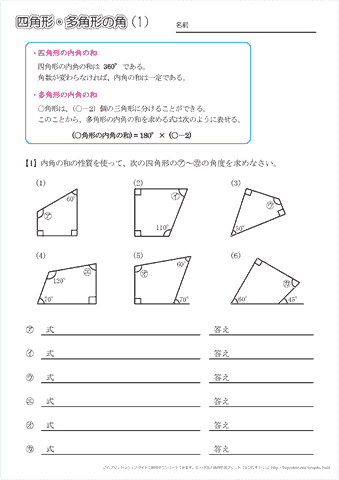
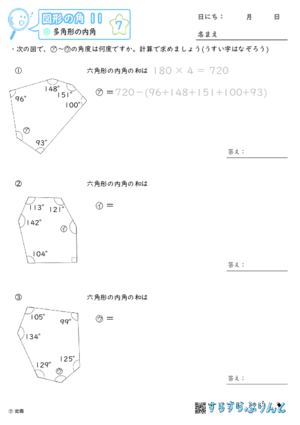
『このような計算式をつかい、こう計算すれば多角形の内角の和が求められる』っていう風に覚えるしかないので、深く考えないほうがいいですよ。 ちなみに三角形は 180度×（3－2）＝180度。 四角形は 180度×（4－2）＝360度 五角形は 180度×（5－2）＝540度。 六角形は 180度×（6－2）＝7度 ですね。 まぁ、公式は覚えるしかない。 で、適所で使えるように練の内角の和はいくつになるのでしょうか。 角形の内角の和の公式＝180× ( －2) ※ 絶対に覚えておいて下さい。 2 正 角形の1つの内角の大きさを求める！ 正三角形の1つの内角の大きさは60度 , 正四角形 (正方形)の1つの内角の大きさは90度です。 五角形 三角形の内角と外角の関係から ＝ ＋ 角A＝30°＋90°＝1° と計算できます。 次に 角B はどうでしょうか。 右の図のように 角B は三角形 ア 、 ウ 、 オ の内角の一つになっています。 三角形の内角の和は180°なので、 角B＝180°－（30°＋45°） ＝180°－75° ＝105° と計算できます。 この角Aように、あらかじめわかる角度を図に記入して、三角形の内角と外角の関係（三角の旗）を
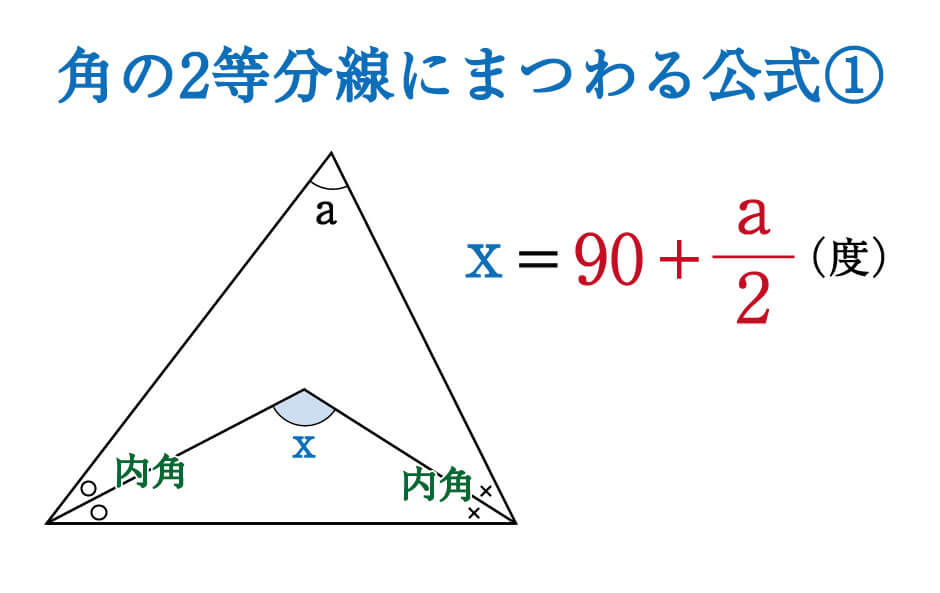
こんにちは、ウチダです。 今日は数学a「図形の性質」で習う 「三角形の内心」 について、性質の証明や基本的な使い方(角の二等分線と比)、座標の求め方や位置ベクトル表示などをわかりやすく解説していきたいと思います。 外心に関する記事と内容がか下図の内角Aの値を求めてみましょう。 A以外の内角の和＝5050＝100度です。 よって、A=180－100＝80度です。 また2つの内角が等しい、3つの内角が等しい三角形では、未知数が2つ以上でも求めることができます。 下図の二等辺三角形の頂角を40度とします。 内角をAとします。 2つの内角は等しいですから、 =180 2A=140 A＝70度 です。 スポンサーリンク 内角の和の値と2－4－1 星型多角形の内角の和 教材（問題場面） 図のように5つの点A，B，C，D， Eがある。点Aから左回りに1つとば しで点を順に結んでいくと星形五角形 ができる。その内角（∠a～∠e）の和 をいろいろな方法で求めてみよう。 H
内角の求め方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 内角の和 算数用語集 |  内角の和 算数用語集 |  内角の和 算数用語集 |
 内角の和 算数用語集 |  内角の和 算数用語集 | 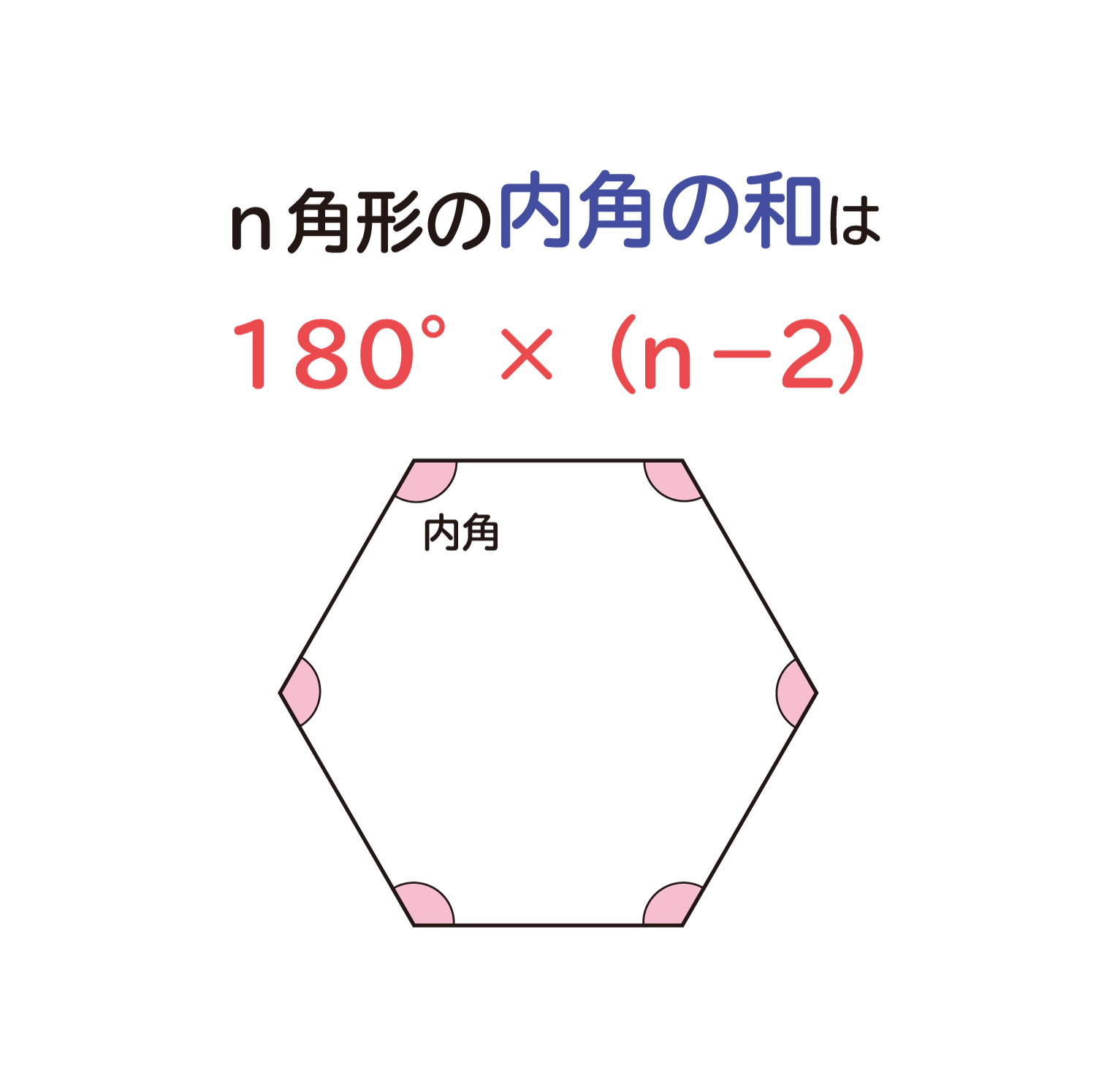 内角の和 算数用語集 |
 内角の和 算数用語集 |  内角の和 算数用語集 | 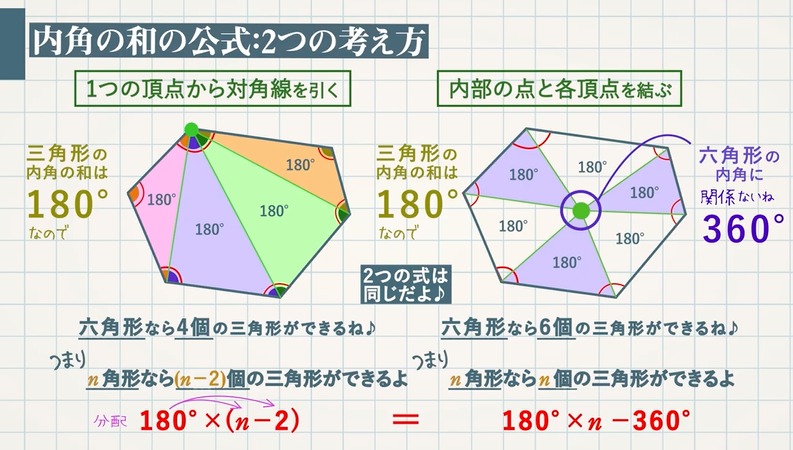 内角の和 算数用語集 |
「内角の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 内角の和 算数用語集 |  内角の和 算数用語集 |  内角の和 算数用語集 |
 内角の和 算数用語集 | 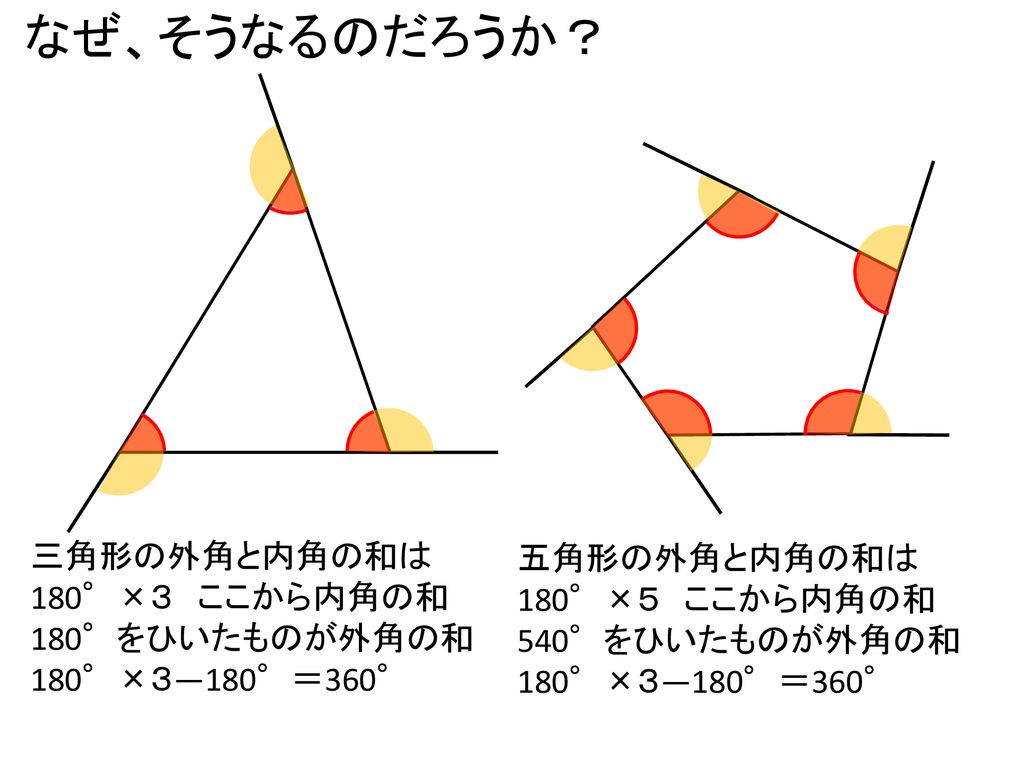 内角の和 算数用語集 | 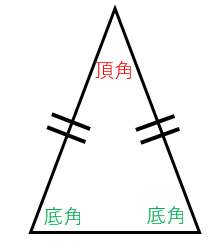 内角の和 算数用語集 |
 内角の和 算数用語集 |  内角の和 算数用語集 |  内角の和 算数用語集 |
「内角の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 内角の和 算数用語集 |  内角の和 算数用語集 | 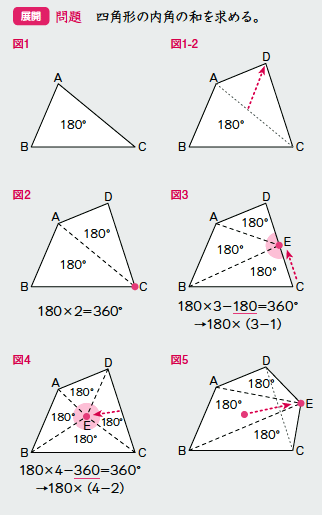 内角の和 算数用語集 |
 内角の和 算数用語集 |  内角の和 算数用語集 |  内角の和 算数用語集 |
 内角の和 算数用語集 | 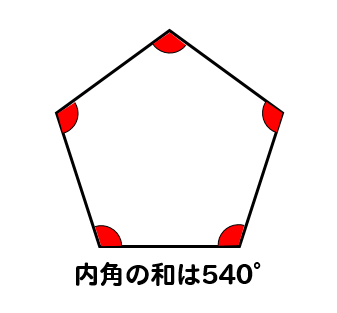 内角の和 算数用語集 |  内角の和 算数用語集 |
「内角の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 内角の和 算数用語集 |  内角の和 算数用語集 |  内角の和 算数用語集 |
 内角の和 算数用語集 |  内角の和 算数用語集 |  内角の和 算数用語集 |
 内角の和 算数用語集 |  内角の和 算数用語集 |  内角の和 算数用語集 |
「内角の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 内角の和 算数用語集 | 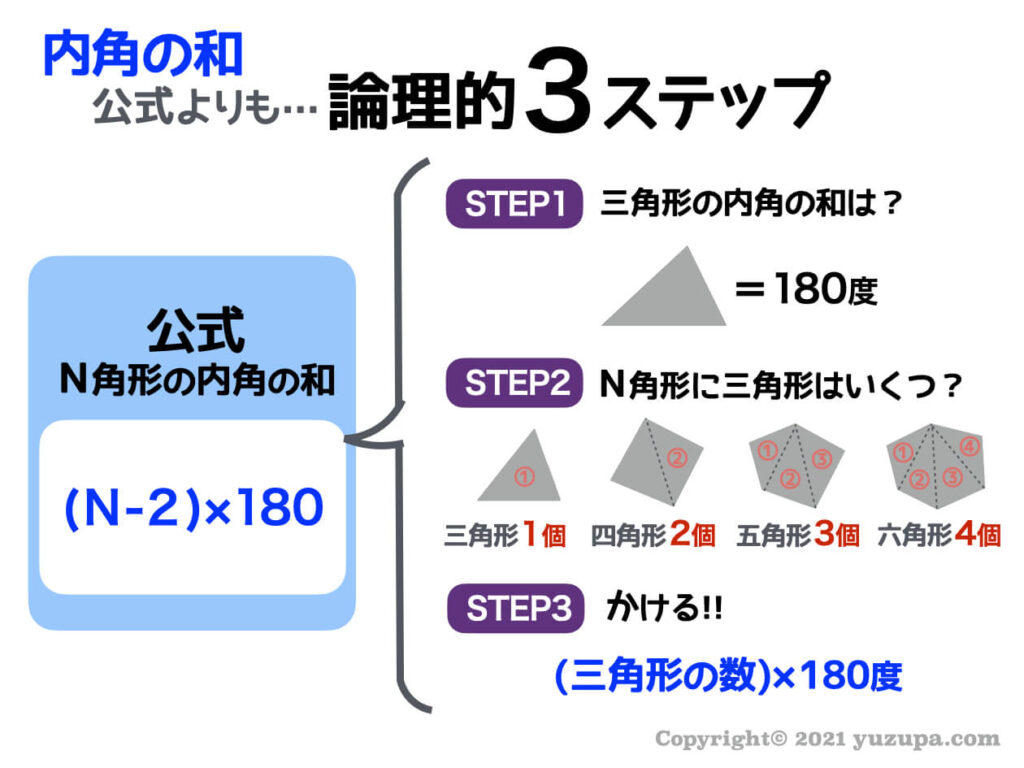 内角の和 算数用語集 | 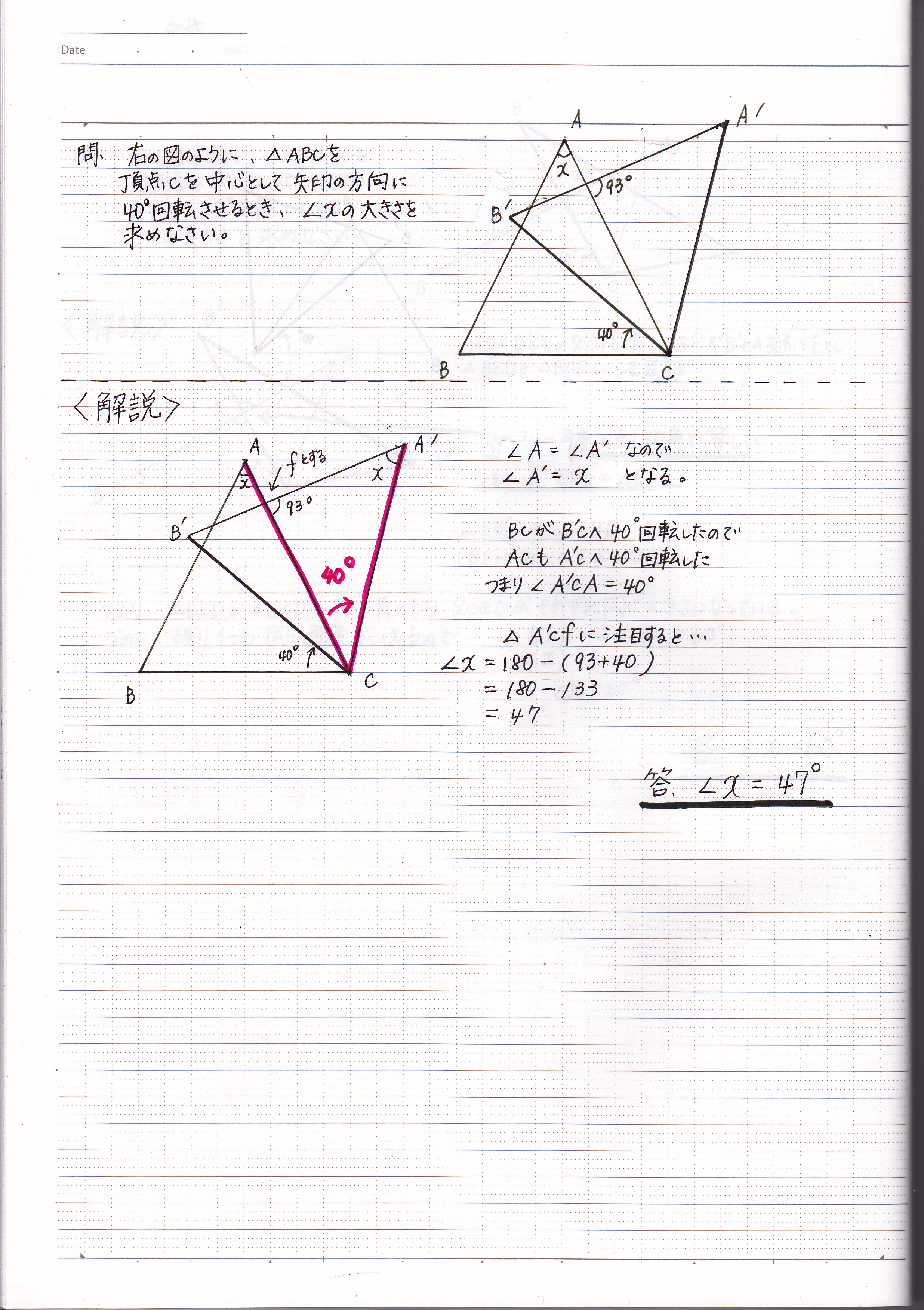 内角の和 算数用語集 |
 内角の和 算数用語集 | 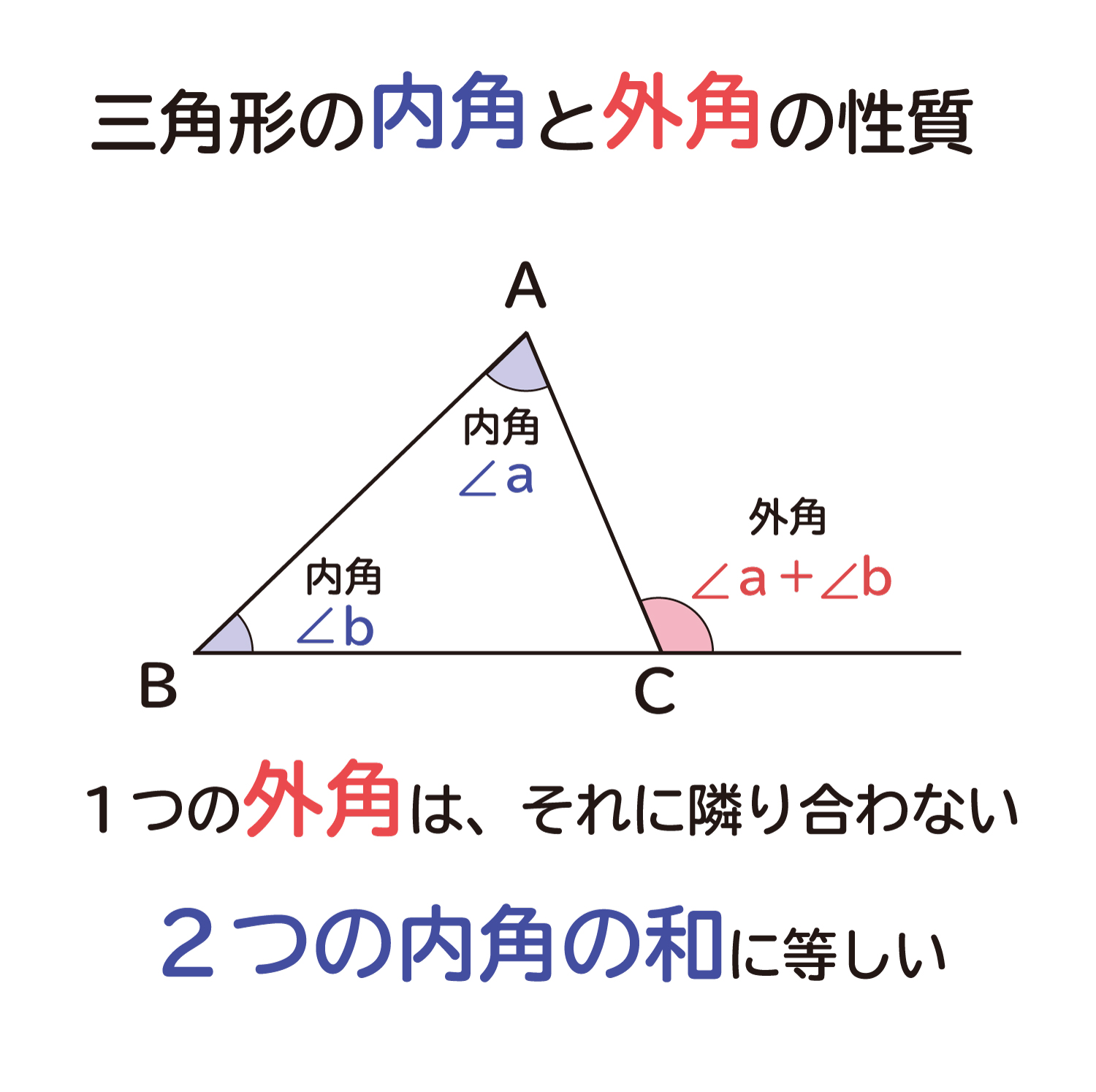 内角の和 算数用語集 |  内角の和 算数用語集 |
 内角の和 算数用語集 |  内角の和 算数用語集 |  内角の和 算数用語集 |
「内角の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 内角の和 算数用語集 |  内角の和 算数用語集 |  内角の和 算数用語集 |
 内角の和 算数用語集 | 内角の和 算数用語集 |  内角の和 算数用語集 |
 内角の和 算数用語集 |  内角の和 算数用語集 | 内角の和 算数用語集 |
「内角の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 内角の和 算数用語集 |  内角の和 算数用語集 |  内角の和 算数用語集 |
内角の和 算数用語集 |  内角の和 算数用語集 |  内角の和 算数用語集 |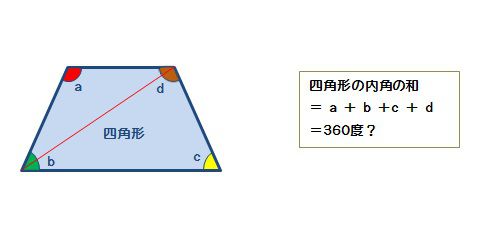
内角の和 算数用語集 | 内角の和 算数用語集 |  内角の和 算数用語集 |
「内角の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
内角の和 算数用語集 |  内角の和 算数用語集 |  内角の和 算数用語集 |
 内角の和 算数用語集 |  内角の和 算数用語集 | 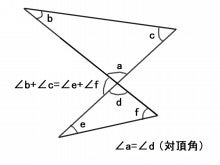 内角の和 算数用語集 |
 内角の和 算数用語集 |  内角の和 算数用語集 |  内角の和 算数用語集 |
「内角の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 内角の和 算数用語集 |  内角の和 算数用語集 | 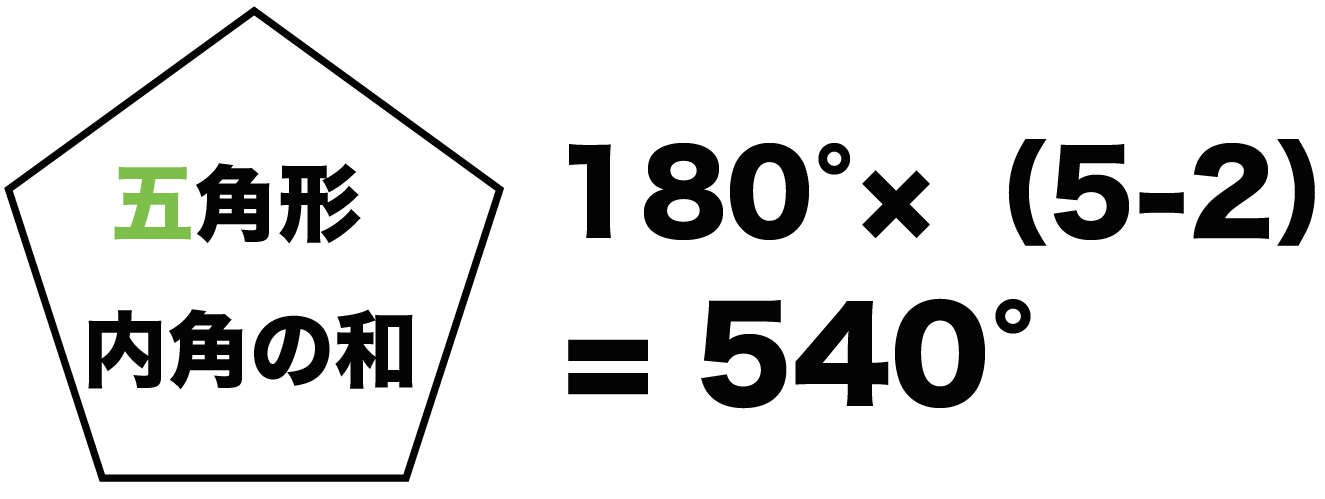 内角の和 算数用語集 |
 内角の和 算数用語集 |  内角の和 算数用語集 | 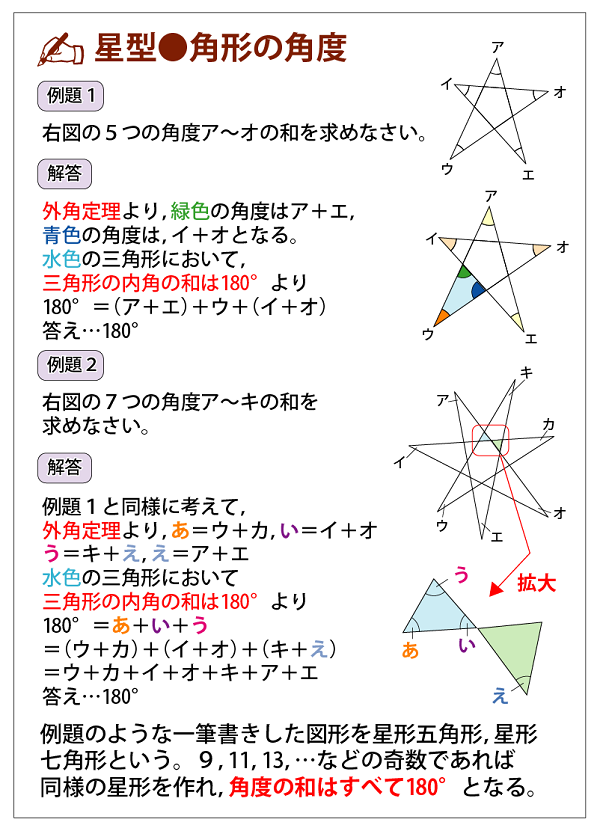 内角の和 算数用語集 |
 内角の和 算数用語集 |  内角の和 算数用語集 |  内角の和 算数用語集 |
「内角の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 内角の和 算数用語集 |  内角の和 算数用語集 |  内角の和 算数用語集 |
 内角の和 算数用語集 |  内角の和 算数用語集 |  内角の和 算数用語集 |
 内角の和 算数用語集 | 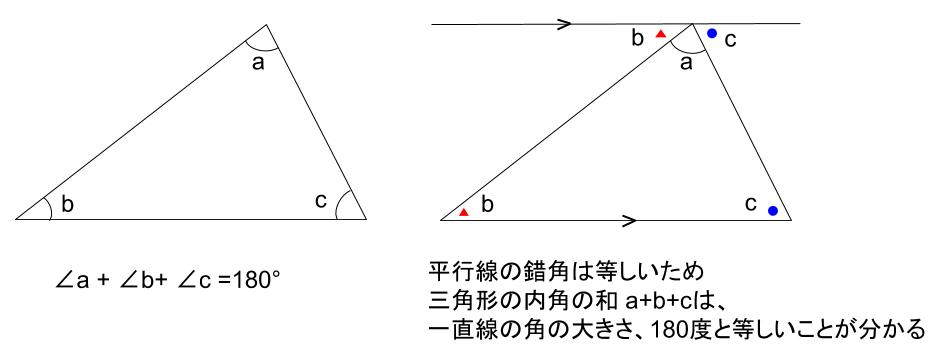 内角の和 算数用語集 | 内角の和 算数用語集 |
「内角の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 内角の和 算数用語集 |  内角の和 算数用語集 | 内角の和 算数用語集 |
内角の和 算数用語集 |  内角の和 算数用語集 |  内角の和 算数用語集 |
 内角の和 算数用語集 |  内角の和 算数用語集 |  内角の和 算数用語集 |
「内角の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 内角の和 算数用語集 | 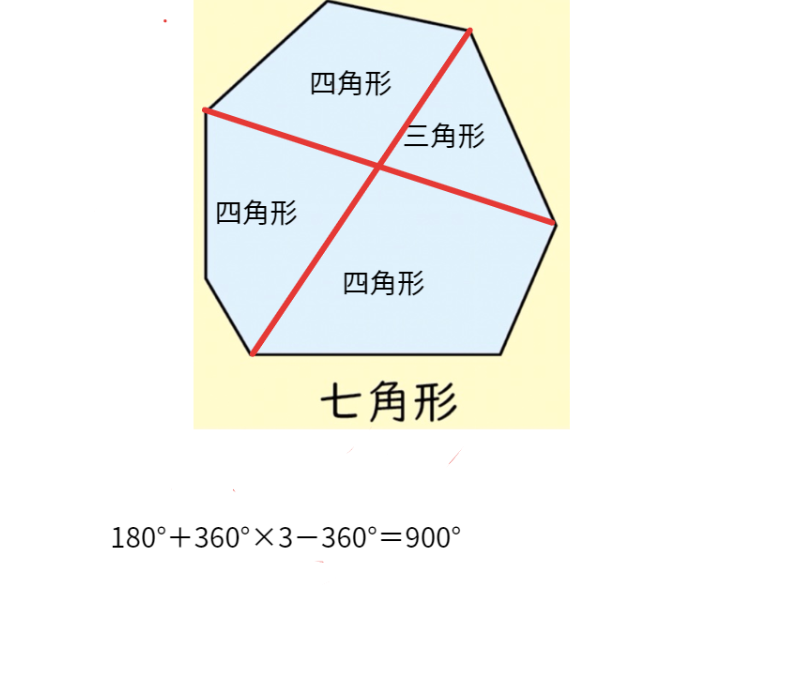 内角の和 算数用語集 |  内角の和 算数用語集 |
 内角の和 算数用語集 |  内角の和 算数用語集 |
阪神正捕手争いの行方は？ 「梅野に求められるのは内角球の有効な使い方」と高代氏 阪神・梅野 このオフ、FA権を行使せずに阪神残留を決め 正二十角形の一つの内角の大きさを求めよ。 二十角形の内角の和は 180× （−2） 180 × （ − 2 ） です。 正多角形はすべての角の大きさが等しいので、これをで割ります。 180× （−2）÷ ＝9 ×18＝162° 180 × （ − 2 ） ÷ ＝ 9 × 18 ＝ 162 ° 答えは 162° 162 ° です。 平面図形の角や面積などの問題は掛け算や割り算が複雑になってくるので、計算の順番などを工夫
Incoming Term: 内角の求め方, 内角の求め方 公式,
コメント
コメントを投稿